MA0301/README.md

MA0301 - Spring 2021 - Diskret Matematikk

Using styling files from oysteikt/texmf

Exercises

Num	Exercise PDF	Answer PDF	Solutions PDF
1	wiki.math.ntnu.no	ex1.pdf	wiki.math.ntnu.no
2	wiki.math.ntnu.no	ex2.pdf	wiki.math.ntnu.no
3	wiki.math.ntnu.no	ex3.pdf	wiki.math.ntnu.no
4	wiki.math.ntnu.no	ex4.pdf	wiki.math.ntnu.no
5	wiki.math.ntnu.no	ex5.pdf	wiki.math.ntnu.no
6	wiki.math.ntnu.no	ex6.pdf	wiki.math.ntnu.no
7	wiki.math.ntnu.no	ex7.pdf	wiki.math.ntnu.no
8	wiki.math.ntnu.no	ex8.pdf	wiki.math.ntnu.no
9	wiki.math.ntnu.no	ex9.pdf	wiki.math.ntnu.no
10	wiki.math.ntnu.no	ex10.pdf	wiki.math.ntnu.no
11	wiki.math.ntnu.no	ex11.pdf	wiki.math.ntnu.no
12	wiki.math.ntnu.no	ex12.pdf	wiki.math.ntnu.no

---

Automation

---

VSCode snippets

See snippets for LaTeX

See snippets for Makefile

---

Chrome plugin

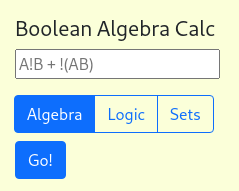
Chapter 1. 2. 3. Boolean calculator

Automates calculating boolean expression step by step by running the input through https://boolean-algebra.com/

Outputs the resulting set of expressions to either propositional logic, boolean algebra or set operations.

Converts output to LaTeX

• Finished

NOTE: there are some bugs when converting boolean algebra AND operations to PL/S

Chapter 4. Induction

Automates proof by induction by running the input through https://wolframalpha.com/

Converts output to LaTeX

• Finished

Chapter 6. Combinatorics

Permutations / Combinations Calculator

Computes permutations and combinations

Outputs to LaTeX

• Finished

---

Python framework

See examples of what the engine for the exam template can do here: exam_template_graphics.pdf

Chapter 1. Truthtables (propositional logic)

Capabilities:

• Calculate and render truthtable for propositional logic expressions

Chapter 3. Sets

Capabilities:

• Calculate and output powersets

Chapter 5. Relations

Capabilities:

Proofs:

• Check whether relation is reflexive
• Check whether relation is symmetric
• Check whether relation is antisymmetric
• Check whether relation is transitive
• Check whether relation is an equivalence relation
• Check whether relation is a partial order

Graphs:

• Draw a hasse diagram from a partial order
• Draw an graph from any relation

Note: Checking whether a relation has a property in this context means that it goes over every pair of related elements and looks for contradictions. This program can not prove relation properties algebraically

Chapter 6. Combinatorics

Capabilities:

• Make an inclusion exclusion expression from list of conditions

Chapter 7. Graph theory

Capabilities:

Inputs:

• Input a graph from a matrix
• Input a graph from a node/edge list
• Input a complete graph from a node number

Outputs:

• Output a graph to a matrix
• Draw an undirected graph
• Draw a directed graph
• Find a minimal spanning tree with Kruskals algorithm

Chapter 8. Finite state automata

Capabilities:

• Draw a finite state machine
• Output a finite state machine table
• Calculate input based on a finite state machine

Python

Capabilities:

• Include a raw python program, and capture its output into a listing