4.8 KiB
Tilstand og oppførsel – Rectangle
Oppgaven handler om en Rectangle-klasse, som håndterer et firkantet område i et koordinatsystem, med sider parallelle med koordinataksene.
Tilstanden i Rectangle-objekter er ikke spesifisert eksplisitt, men må velges slik at metodene nedenfor kan implementerers. Merk at alle metodene jobber med heltallsstørrelser.
Rectangle-klassen har metoder for å spørre om tilstanden og endre tilstanden. Spørremetodene dekker høyde og bredde og koordinatene til øverste venstre og nederste høyre hjørne og om rektanglet inneholder spesifikke punkt(er). Endringsmetodene dekker utviding ved å legge til punkter.
Merk: Rectangle-klassen fungerer som om du krysser ut et rutenett, altså at et punkt ("kryss") har en lengde og bredde på 1, ikke som i matematikk der punkter ikke har størrelser. Bildeserien under viser et eksempel på hvordan bredde og høyde endres når man legger til punkter i rektangelet.
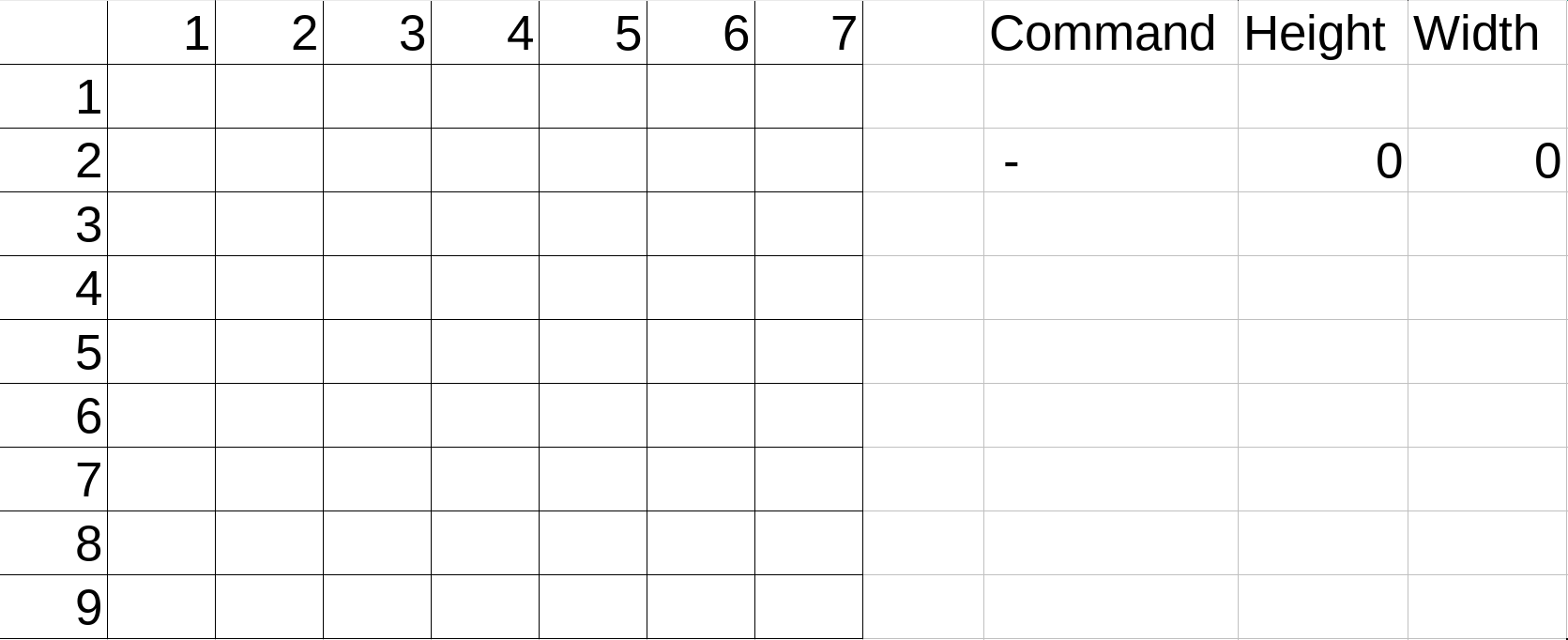



Logikken til metodene må tilfredsstille følgende krav:
- et
Rectangle-objekt er tomt i starten - et tomt
Rectangle-objekt skal returnere`0`for alleget-metodene (minX,minY,maxX,maxY),trueforisEmptyogfalseforcontains-metodene. - et punkt har bredde og høyde lik
`1`, så dersom en legger punktet`(x,y)`til et tomtRectangle-objekt, så skalgetMinXoggetMaxXreturnere`x`,getMinYoggetMaxYskal returnere`y`oggetWidthoggetHeightskal returnere`1`. - når en utvider et
Rectangle-objekt med en avadd-metodene, så skal ikke rektanglet bli større enn nødvendig.
Spørremetoder:
int getMinX()ogint getMinY()- returnerer henholdsvis $x$- og $y$-koordinatene til punktet med lavest $(x,y)$-verdier som er inneholdt i dette rektanglet. Dersom dette rektanglet er tomt, så skal`0`returneres.int getMaxX()ogint getMaxY()- returnerer henholdsvis $x$- og $y$-koordinatene til punktet med høyest $(x,y)$-verdier som er inneholdt i dette rektanglet. Dersom dette rektanglet er tomt, så skal`0`returneres.int getWidth()ogint getHeight()- returnerer henholdsvis bredden og høyden til rektanglet. Begge skal returnere`0`, dersom dette rektanglet er tomt.boolean isEmpty()- returnerertrueom rektanglet er tomt, dvs. om bredden og/eller høyden er`0`.boolean contains(int x, int y)- returnerertrueom punktet`(x,y)`er inneholdt i dette rektanglet, ogfalseellers.boolean contains(Rectangle rect)- returnerertrueom helerect, dvs. alle punktene irect, er inneholdt i dette rektanglet, og false ellers. Dersomrecter tomt, så skalfalsereturneres.
Endringsmetoder:
boolean add(int x, int y)- utvider (om nødvendig) dette rektanglet slik at det (akkurat) inneholder punktet`(x,y)`. Etter kallet skal altsåcontains(x, y)returneretrue. Returnerertrueom dette rektanglet faktisk ble endret, ellersfalse.boolean add(Rectangle rect)- utvider (om nødvendig) dette rektanglet slik at det (akkurat) inneholder helerect-argumentet. Returnerertrueom dette rektanglet faktisk ble endret, ellersfalse. Dersomrecter tomt, så skal dette rektanglet ikke endres.
Andre metoder:
Rectangle union(Rectangle rect)- returnerer et nyttRectangle-objekt som tilsvarer kombisjonen av dette rektanglet ogrect-argumentet. Alle punktene som finnes i ett av rektanglene skal altså være inneholdt i rektanglet som returneres.
Del 1 - Tilstandsdiagram
Tegn et objekttilstandsdiagram for en tenkt bruk av Rectangle-klassen. Velg en sekvens av kall som bruker alle fire endringsmetoder.
Del 2 - Java-kode
Skriv Java-kode for Rectangle-klassen med oppførsel som er beskrevet over.
Lag en passende toString()-metode og et hovedprogram, slik at du kan sjekke at oppførselen stemmer med tilstandsdiagrammet (bruk samme sekvens av kall).
Testkode for denne oppgaven finner du her: src/test/java/stateandbehavior/RectangleTest.java.
Ekstraoppgave
Implementer følgende metoder:
Rectangle intersection(Rectangle rect)- returnerer et nyttRectangle-objekt som tilsvarer overlappet mellom dette rektanglet ogrect-argumentet. Alle punktene som finnes i begge rektanglene skal altså være inneholdt i rektanglet som returneres.boolean intersects(Rectangle rect)- returnerertrueom dette rektanglet ogrect-argumentet overlapper, dvs. om det finnes ett eller flere punkter som er inneholdt i begge disse rektanglene.